Questo articolo spiega che cosa sono e come si costruiscono le carte di controllo per variabili.
Carte di controllo per variabili
Carta media-range (x-R)
Rappresentano il tipo più diffuso e consentono di rappresentare un processo in cui l’output è misurato secondo una grandezza variabile e continua (lunghezza, peso, durezza, conduttività, .). Si usa, solitamente, nel caso in cui le misurazioni inerenti ogni campione rispettino la condizione ![]() .
.
Si realizzano due carte con nelle quali si rappresentano, rispettivamente, la media e il range di ogni campione dopo aver fissato i seguenti valori:
- carta della media;
- carta dei range.
Sulla carta delle medie si fissano i seguenti limiti (rispettivamente superiore, centrale ed inferiore):
(1) 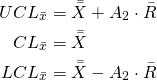
mentre nella carta dei range i seguenti:
(2) 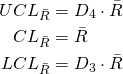
Carta della media e della deviazione standard (x-sigma)
Indicativamente viene spesso utilizzata nel caso complementare al precedente ovvero quando n > 10.
Similmente alla precedente si rappresenta la media e la sigma di ogni campione analizzato in due carte distinte in cui sono rappresentati i seguenti valori:
- carta della media;
- carta della deviazione standard.
Analogamente al tipo di carta precedente, vengono posti dei limiti nella carta delle merdie
(3) 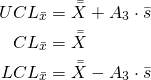
e nella carta delle deviazioni standard
(4) 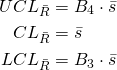
Carta di controllo per misurazioni singole
Nella pratica operativa può capitare che il processo non permetta di ottenere campioni con numerosità maggiore di un singolo elemento (cioè il campione è n=1). In questo caso non ha senso parlare di media e nemmeno di range quindi viene utilizzata un’altra tecnica per la rappresentazione del processo in una carta di Sheward.
Dato che la costruzione di questa carta ha delle problematiche diverse dalle altre due precedentemente affrontate verrà trattata in uno dei prossimi articoli.

Lascia un commento